The Golden Ratio at your Dinner Table
by
Michael S. Schneider
author of A Beginner's Guide To Constructing The Universe and six accompanying workbooks.
If you're sitting around the kitchen or waiting for your meal at a restaurant (and you're mathematically inclined)
you might marvel at this unexpected appearance of the famous Golden Ratio first discovered and expressed in marvelous ways by the artist Jo Niemeyer.
Gather three identical knives (or straws, breadsticks or any other identical lengths) and find the center of two of them.
Place one vertically and then put another's tip at it's middle point, so that they lie along the same horizontal bottom line.
Then place the tip of the third knife at the center of the second knife, and rotate it down to the same bottom line.
 Believe it or not, the distances along the bottom horizontal line form the Golden Ratio,
where the whole length (A+B) relates to the large part (A) as the large part (A) relates to the small part (B)!
It's a perfect mathematical balance relating the parts to each other and to the whole by the same, unifying rule.
The Golden Ratio is the source of elegant balance throughout the universe, from atoms to galaxies.
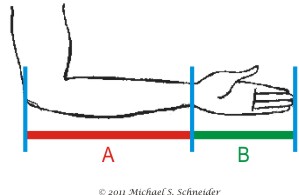
The nearest place to notice it is the length of your "cubit" from elbow to fingertip,
where our wrist marks the Golden Ratio division:
Believe it or not, the distances along the bottom horizontal line form the Golden Ratio,
where the whole length (A+B) relates to the large part (A) as the large part (A) relates to the small part (B)!
It's a perfect mathematical balance relating the parts to each other and to the whole by the same, unifying rule.
The Golden Ratio is the source of elegant balance throughout the universe, from atoms to galaxies.
The nearest place to notice it is the length of your "cubit" from elbow to fingertip,
where our wrist marks the Golden Ratio division:
 Here's the mathematical proof of the Golden Ratio "knife arrangement":
The arrangement of three identical knives can be seen as three blue lines (see illustration below).
The leftmost blue line is at a right angle to the black horizontal line at its bottom.
Each "knife" touches the center of the one to its left.
The bottom of the three line segments fall along the same horizontal line at bottom:
Here's the mathematical proof of the Golden Ratio "knife arrangement":
The arrangement of three identical knives can be seen as three blue lines (see illustration below).
The leftmost blue line is at a right angle to the black horizontal line at its bottom.
Each "knife" touches the center of the one to its left.
The bottom of the three line segments fall along the same horizontal line at bottom:
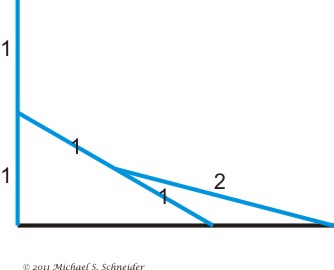 In this arrangement (seen below) we can identify a triangle (red) whose side is 1 and hypotenuse is 2.
Using the Pythagorean Theorem, we find the remaining side to equal the square root of 3.
(It's half an equilateral triangle, admired by Plato in his Timeaus as the most beautiful triangle.)
In this arrangement (seen below) we can identify a triangle (red) whose side is 1 and hypotenuse is 2.
Using the Pythagorean Theorem, we find the remaining side to equal the square root of 3.
(It's half an equilateral triangle, admired by Plato in his Timeaus as the most beautiful triangle.)
 Another part of the arrangement can be seen as a different triangle having side 1/2 and hypotenuse equaling 2.
Using the Pythagorean Theorem again, we find that the remaining side at the bottom equals half the square root of 15.
Another part of the arrangement can be seen as a different triangle having side 1/2 and hypotenuse equaling 2.
Using the Pythagorean Theorem again, we find that the remaining side at the bottom equals half the square root of 15.
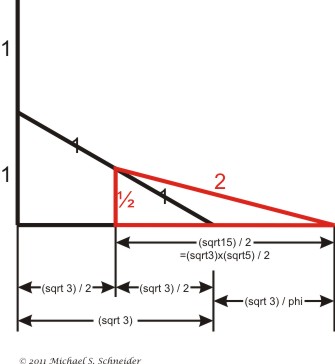 The square root of 3 length has been naturally divided into halves by the left side of this triangle.
To find the length remaining to the right of the sqrt 3 length we have to recognize that the square root of 15 equals the square root of 3 times the square root of 5.
The remaining difference can be found by subtracting half the square root of 3 from half the square root of 15:
(sqrt 15)/2 - (sqrt 3)/2
= (sqrt 3)(sqrt 5)/2 - (sqrt 3)/2
= (sqrt 3)/2 (sqrt 5 - 1)
= (sqrt 3) (sqrt 5 - 1)/2
Since (sqrt 5 - 1)/2 is the definition of the inverse of the Golden Ratio or 1/Phi (= 0.618...)
the length of this section equals (the square root of 3)/Phi:
The square root of 3 length has been naturally divided into halves by the left side of this triangle.
To find the length remaining to the right of the sqrt 3 length we have to recognize that the square root of 15 equals the square root of 3 times the square root of 5.
The remaining difference can be found by subtracting half the square root of 3 from half the square root of 15:
(sqrt 15)/2 - (sqrt 3)/2
= (sqrt 3)(sqrt 5)/2 - (sqrt 3)/2
= (sqrt 3)/2 (sqrt 5 - 1)
= (sqrt 3) (sqrt 5 - 1)/2
Since (sqrt 5 - 1)/2 is the definition of the inverse of the Golden Ratio or 1/Phi (= 0.618...)
the length of this section equals (the square root of 3)/Phi:
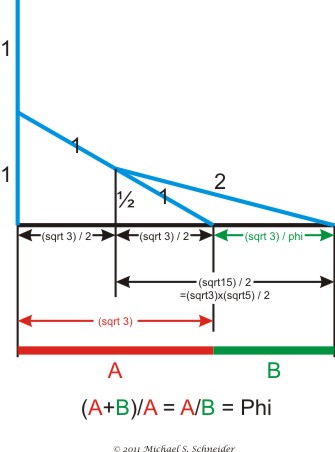 The square root of 3 (length A above) divided by (the square root of three over Phi, length B above) simply equals Phi, the Golden Ratio.
Q.E.D.
This fascinating mathematical ratio consistently appears in the most surprising places!
The Golden Ratio, which is essentially an appearance of the square root of 5,
appeared here with its cousin the square root of 3.
This shouldn't be too surprising if you know that the Golden Ratio actually emerges from an inscribed equilateral triangle
in a way that also involves the midpoints of three identical lines (the sides of the triangle):
The square root of 3 (length A above) divided by (the square root of three over Phi, length B above) simply equals Phi, the Golden Ratio.
Q.E.D.
This fascinating mathematical ratio consistently appears in the most surprising places!
The Golden Ratio, which is essentially an appearance of the square root of 5,
appeared here with its cousin the square root of 3.
This shouldn't be too surprising if you know that the Golden Ratio actually emerges from an inscribed equilateral triangle
in a way that also involves the midpoints of three identical lines (the sides of the triangle):
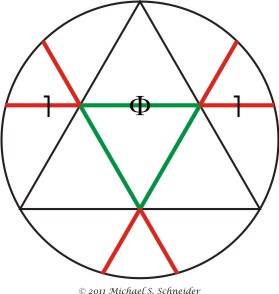 Any of the three green line segments relates to any of the six red segments in the Golden Ratio.
But that's another of the Golden Ratio's stories!
Text and Illustrations (c) 2011-12 Michael S. Schneider
The source of this wonderful construction is the artist Jo Niemeyer.
Constructing The Universe Home Page
Any of the three green line segments relates to any of the six red segments in the Golden Ratio.
But that's another of the Golden Ratio's stories!
Text and Illustrations (c) 2011-12 Michael S. Schneider
The source of this wonderful construction is the artist Jo Niemeyer.
Constructing The Universe Home Page
 Believe it or not, the distances along the bottom horizontal line form the Golden Ratio,
where the whole length (A+B) relates to the large part (A) as the large part (A) relates to the small part (B)!
It's a perfect mathematical balance relating the parts to each other and to the whole by the same, unifying rule.
The Golden Ratio is the source of elegant balance throughout the universe, from atoms to galaxies.
The nearest place to notice it is the length of your "cubit" from elbow to fingertip,
where our wrist marks the Golden Ratio division:
Believe it or not, the distances along the bottom horizontal line form the Golden Ratio,
where the whole length (A+B) relates to the large part (A) as the large part (A) relates to the small part (B)!
It's a perfect mathematical balance relating the parts to each other and to the whole by the same, unifying rule.
The Golden Ratio is the source of elegant balance throughout the universe, from atoms to galaxies.
The nearest place to notice it is the length of your "cubit" from elbow to fingertip,
where our wrist marks the Golden Ratio division:
 Here's the mathematical proof of the Golden Ratio "knife arrangement":
The arrangement of three identical knives can be seen as three blue lines (see illustration below).
The leftmost blue line is at a right angle to the black horizontal line at its bottom.
Each "knife" touches the center of the one to its left.
The bottom of the three line segments fall along the same horizontal line at bottom:
Here's the mathematical proof of the Golden Ratio "knife arrangement":
The arrangement of three identical knives can be seen as three blue lines (see illustration below).
The leftmost blue line is at a right angle to the black horizontal line at its bottom.
Each "knife" touches the center of the one to its left.
The bottom of the three line segments fall along the same horizontal line at bottom:
 In this arrangement (seen below) we can identify a triangle (red) whose side is 1 and hypotenuse is 2.
Using the Pythagorean Theorem, we find the remaining side to equal the square root of 3.
(It's half an equilateral triangle, admired by Plato in his Timeaus as the most beautiful triangle.)
In this arrangement (seen below) we can identify a triangle (red) whose side is 1 and hypotenuse is 2.
Using the Pythagorean Theorem, we find the remaining side to equal the square root of 3.
(It's half an equilateral triangle, admired by Plato in his Timeaus as the most beautiful triangle.)
 Another part of the arrangement can be seen as a different triangle having side 1/2 and hypotenuse equaling 2.
Using the Pythagorean Theorem again, we find that the remaining side at the bottom equals half the square root of 15.
Another part of the arrangement can be seen as a different triangle having side 1/2 and hypotenuse equaling 2.
Using the Pythagorean Theorem again, we find that the remaining side at the bottom equals half the square root of 15.
 The square root of 3 length has been naturally divided into halves by the left side of this triangle.
To find the length remaining to the right of the sqrt 3 length we have to recognize that the square root of 15 equals the square root of 3 times the square root of 5.
The remaining difference can be found by subtracting half the square root of 3 from half the square root of 15:
(sqrt 15)/2 - (sqrt 3)/2
= (sqrt 3)(sqrt 5)/2 - (sqrt 3)/2
= (sqrt 3)/2 (sqrt 5 - 1)
= (sqrt 3) (sqrt 5 - 1)/2
Since (sqrt 5 - 1)/2 is the definition of the inverse of the Golden Ratio or 1/Phi (= 0.618...)
the length of this section equals (the square root of 3)/Phi:
The square root of 3 length has been naturally divided into halves by the left side of this triangle.
To find the length remaining to the right of the sqrt 3 length we have to recognize that the square root of 15 equals the square root of 3 times the square root of 5.
The remaining difference can be found by subtracting half the square root of 3 from half the square root of 15:
(sqrt 15)/2 - (sqrt 3)/2
= (sqrt 3)(sqrt 5)/2 - (sqrt 3)/2
= (sqrt 3)/2 (sqrt 5 - 1)
= (sqrt 3) (sqrt 5 - 1)/2
Since (sqrt 5 - 1)/2 is the definition of the inverse of the Golden Ratio or 1/Phi (= 0.618...)
the length of this section equals (the square root of 3)/Phi:
 The square root of 3 (length A above) divided by (the square root of three over Phi, length B above) simply equals Phi, the Golden Ratio.
Q.E.D.
This fascinating mathematical ratio consistently appears in the most surprising places!
The Golden Ratio, which is essentially an appearance of the square root of 5,
appeared here with its cousin the square root of 3.
This shouldn't be too surprising if you know that the Golden Ratio actually emerges from an inscribed equilateral triangle
in a way that also involves the midpoints of three identical lines (the sides of the triangle):
The square root of 3 (length A above) divided by (the square root of three over Phi, length B above) simply equals Phi, the Golden Ratio.
Q.E.D.
This fascinating mathematical ratio consistently appears in the most surprising places!
The Golden Ratio, which is essentially an appearance of the square root of 5,
appeared here with its cousin the square root of 3.
This shouldn't be too surprising if you know that the Golden Ratio actually emerges from an inscribed equilateral triangle
in a way that also involves the midpoints of three identical lines (the sides of the triangle):
 Any of the three green line segments relates to any of the six red segments in the Golden Ratio.
But that's another of the Golden Ratio's stories!
Text and Illustrations (c) 2011-12 Michael S. Schneider
The source of this wonderful construction is the artist Jo Niemeyer.
Constructing The Universe Home Page
Any of the three green line segments relates to any of the six red segments in the Golden Ratio.
But that's another of the Golden Ratio's stories!
Text and Illustrations (c) 2011-12 Michael S. Schneider
The source of this wonderful construction is the artist Jo Niemeyer.
Constructing The Universe Home Page